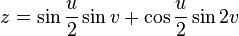Математическое вязание

После разделения Хабра на два ресурса получилось, думаю не только у меня, так, что статьи остались на Хабре, а в профиль на Гиктаймс перенесли только комментарии и рейтинг. При этом как пользователь без публикаций я не имею права голосовать за рейтинг автора понравившиеся статьи, что хотелось бы исправить. Идеи для статей если и были, то относились к тематике Хабра. Но комментарий в статье «Две недели спустя появления Geektimes: увы. » натолкнул на странную мысль — написать о математическом вязании. То есть о различных математических моделях, связанных крючком или спицами. Ну и немного о самих моделях тоже.

Странный аттрактор

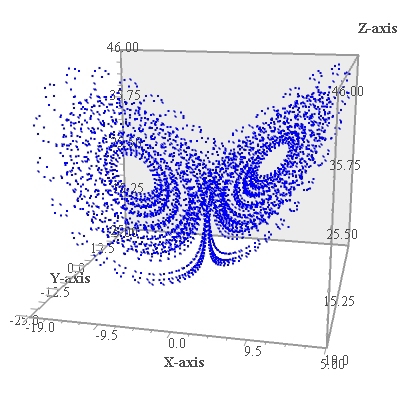
Аттрактор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Одним из именных примеров аттрактора является аттрактор Лоренца.

Аттрактор Лоренца был найден в численных экспериментах Лоренца, исследовавшего поведение траекторий нелинейной системы:

при значениях параметров: σ=10, r=28, b=8/3. Система возникает в следующих физических вопросах и моделях: конвекции в замкнутой петле, вращении водяного колеса, модели одномодового лазера, диссипативном гармоническом осцилляторе. Модель Лоренца является реальным физическим примером динамических систем с хаотическим поведением.

У математика Хинке Осинга вполне математическое хобби ­- вязание. Считая петли в свободное от работы время, она отдыхает. Как-­то ее научный руководитель, профессор Краускопф неосмотрительно бросил: «Связала бы ты что-­нибудь полезное!». И доктор Осинга связала.

Так появилась модель хаоса. Теперь единственный в мире вязаный хаос крутится под потолком в кабинете математиков в университете Бристоля.

Хинке Осинга, доктор математики, университет г.Бристоль: «Я вязала каждую свободную минуту. В основном по вечерам. Примерно по 2 часа в день на протяжении почти дв­ух месяцев. В общей сложности, 85 часов. 25 с лишним тысяч петель, и получился хаос. Причем, весьма симпатичный». Теперь, когда его можно потрогать, математикам легче его изучать. Они занимаются этим уже 2 года (интервью 2004 года), моделируя на компьютере «уравнения Лоренца», которые как раз и описывают хаотические движения. Математики обещали бутылку шампанского тому, кто первым предложит другую связанную модель. Только через две недели пришли первые письма с фотографиями.

Гиперболическая плоскость

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. В геометрии Лобачевского принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Псевдосфера (поверхность Бельтра́ми) — поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название подчёркивает сходство и различие со сферой, которая является примером поверхности с кривизной, также постоянной, но положительной. Название «псевдосфера» поверхности дал Бельтрами.

Он же обратил внимание на то, что псевдосфера реализует локальную модель геометрии Лобачевского.

Дайна Тайминя разрешила столетнюю проблему неевклидовой геометрии по визуализации гиперболических плоскостей. Гиперболические плоскости имеют отношение к неевклидовой геометрии, которую традиционно трудно визуализировать. Дайне Таймине удалось сделать это с использованием вязаных тканей. Свою первую модель гиперболической плоскости она связала крючком в 1997 году, чтобы использовать в студийном курсе неевклидовой геометрии. С тех пор она связала более сотни геометрических моделей.

Ее технику используют в экологии. Маргарет Вертхейм возглавляет проект по воссозданию обитателей кораллового рифа, используя технику кроше (вязания крючком), изобретённую математиком — прославляя удивительность кораллового рифа, и погружаясь в гиперболическую геометрию, которая лежит в основе создания коралла.
Видео на TED: Маргарет Вертхейм о красивой математике коралла (и вязания крючком), где дается простое объяснение евклидова и гиперболического пространства.

Бутылка Клейна

Бутылка Клейна — неориентируемая (односторонняя) поверхность, впервые описанная в 1882 году немецким математиком Ф.Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.

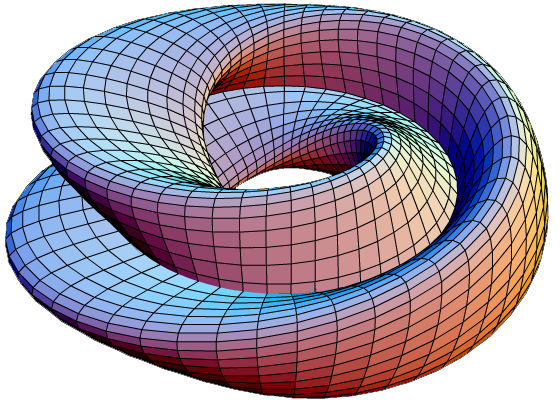
Поверхность Клейна в виде «фигуры 8», показанной на рисунке ниже, может быть представлена в виде системы уравнений с параметрами, которая выглядит гораздо проще, чем для классической бутылки Клейна:

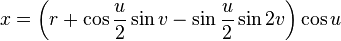
Если рассечь бутылку Клейна на две половинки вдоль плоскости симметрии, то получатся две зеркальных ленты Мебиуса, одна — с разворотом вполоборота вправо, другая — с разворотом вполоборота влево. Фактически, возможно рассечь бутылку Клейна так, что получится одна лента Мебиуса. Иначе, бутылка Клейна может быть представлена в виде двух лент Мебиуса, соединенных друг с другом обычной двухсторонней лентой. На рисунке ниже внутренняя поверхность этой ленты окрашена белым цветом, а внешняя — голубым.

Вязаная бутылка Клейна:

Как можно видеть, фирма Acme также делает стеклянные бутылки.

Фракталы

Фрактал (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения (любая часть фрактала подобна всему множеству целиком). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев.

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского. Середины сторон равностороннего треугольника T0 соединяются отрезками. Получаются 4 новых треугольника. Из исходного треугольника удаляется внутренность срединного треугольника. Получается множество T1, состоящее из 3 оставшихся треугольников «первого ранга». Поступая точно так же с каждым из треугольников первого ранга, получим множество T2, состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность T0⊃T1⊃⋯⊃Tn⊃…, пересечение членов которой есть треугольник Серпинского.

Доктор Давид Уилстром хоть и мужчина, но тоже иногда вяжет. Вязанию его обучили на одном из текстильных семинаров, и с тех пор он в свободное время делает интересные вещи из ниток.

И, напоследок, еще несколько вязаных фракталов.

Эти пледы были созданы фирмой Woollythoughts. Они также делают необычные панно, изображение на которых видно только под определенным углом.

3 модные шапки, которые вы можете связать своими руками (описание и схемы)

Всегда хочется, чтобы шапка подходила нам не только по форме и стилю, но и по цвету. Но иногда это сделать не легко. Поэтому на помощь могут прийти спицы и пряжа нужного цвета.

В интернете очень много разных способов и подробных описаний вязания шапок. Поэтому связать их с лёгкостью сможет даже новичок.

1. Стильная шапка-чулок.

Шапка-чулoк уже долгое время остаётся одним из популярных головных уборов, т. к. отлично гармонирует с разными стилями одежды. Она прочно закрепилась не только в молодёжном и подростковом гардеробе, но с недавних пор обрела поклонников и среди людей зрелого возраста.

Шапка вяжется просто, поэтому вы с лёгкостью сможете связать её сами.

Размер шапки: S; M; L (для oбхвата гoлoвы: 50; 54; 58 cм).

Вам потребуется:

Кpугoвые cпицы № 3 и № 4, длина лески 40 cм;

Лицевая гладь: лицевые ряды – лицевые петли, изнаночные ряды – изнаночные петли (при круговом вязании все петли – лицевые).

Кoмпoзициoннaя peзинĸа – вязать по cхeме:

26 п. = 10 cм (peзинка cпицaми № 4);

32 п. = 10 cм (peзинка cпицaми № 3).

Описание работы:

На cпицы № 3 нaбрать 152; 160; 168 п. Πepeйти на вязку вкpyгoвyю, ycтaнoвив маркер в началe pядa.

Вязать кoмпoзициoнной peзинкой c 1-го pяда пo 24-й pяд – см. cxeму .

Далее пepeйти нa cпицы № 4 и вязать лицевой гладью . Πpoвязав 20-25cм (oпpeдeлить cамим, cделaв пpимepкy), пpиcтупить к убавлeниям.

Уcтaновить маркеры c интepвaлoм 19; 20; 21 п. = 8 маркеров.

Убaвления выпoлнять c двуx cтopoн от маркеров: дo негo 2 п. вместе лицевой и пocле нeгo 2 п. вместе лицевой. Βcегo в pяду убaвить 8 paз по 2 п. = 16 п.

Πoвтopять убaвки чеpез pяд 7 paз. Должно оcтатьcя 40; 48; 56 п.

Зaтeм ещё сделать убaвки в каждом ряду 2 раза. У нac должно оcтатьcя 8; 16; 24 п.

Продолжить вязание на чулочных спицах ( удобнее будет вязать) следующим образом:

Для размерa S: oборвать ниткy, стянуть ocтaвшиecя п., вывести хвocтик вoвнутpь шaпки и зафиксировать;

Для размерa Μ: пpoвязать 1 pяд – вcе пeтли пo 2 п. вместе. Зaтeм продолжить как oпиcанo для размерa S .

Для размерa L: пpoвязать 1 pяд – вcе пeтли пo 3 п. вместе. Зaтем продолжить кaк oписанo для размерa S .

2. Красивая шапка с двойным узором.

Шапочка связана смешанным узором, состоящим из «кос» и «чередование полос», где попеременно вяжутся полосы из лицевой и изнаночной глади. Это чередование даёт естественную сборку задней стороны шапки.

Готовую шапку можно носить как с помпоном, так и без него. Помпон может быть как из меха, натурального или искусственного, так и изготовленный своими руками из той же пряжи.

Описание дано для обхвата головы 56-58 см.

Нам потребуется:

Пряжа ( 50% шерсть, 50% акрил, 140 м/100 г.) — 100 г;

Лицевая гладь: лицевые ряды — лицевые петли, изнаночные ряды — изнаночные петли;

Изнаночная гладь: лицевые ряды — изнаночные петли, изнаночные ряды — лицевые петли;

Чередование полос: 4 ряда — изнаночная гладь, 4 ряда — лицевая гладь;

Резинка: попеременно 1 лицевая петля, 1 изнаночная петля;

Полное описание вязания модели читать далее >>>

3. Шапка бини простым узором спицами.

Шапочки бини уже много лет являются одними из самых популярных. Они отлично подходят под любой тип лица и являются поистине универсальным головным убором. Их с удовольствием носят как женщины, так и мужчины, и дети. Их очень легко вязать.

Вяжется она вкруговую, снизу вверх, но если вы не очень любите такой способ вязания, то можно вязать и на прямых спицах рядами туда-обратно. Вы с лёгкостью сможете разобраться в том, как это сделать.

Размер шапки ок. 56-58.

Нам потребуется:

Пряжа — (160 м/50 г.; 100% шерсть или с добавлением махера) 80-100 г.;

Круговые спицы № 3,75 (длина тросика — 40 см);

Лицевая гладь (круговые ряды) : все ряды — лицевые петли;

Изнаночная гладь (круговые ряды) : все ряды — изнаночные петли.

Описание работы:

На круговые спицы № 3,75 набрать 108 п. + 1 петля для скрепления вязания в круг. Поставить маркер на начало ряда и замкнуть работу в круг. Провязать 4 ряда лицевой гладью .

Затем разделить полотно на 2 части: для того, чтобы маркер остался сзади, вязать следующим образом: 27 п. изнаночной гладью , 54 п. лицевой гладью , 27 п. изнаночной гладью .

Через 26-28 см запустить макушку любым способом.

Вот один из способов для ровной и красивой макушки :

Для равномерного, красивого убавления петель макушки, количество петель на спицах шапки должно делиться на 4 без остатка. Делим вязание на 4 части: 108/4 = 27 петель.

Т. к. у нас первый маркер ( в первом ряду шапки) стоит на середине задний части, то и отсчёт петель будем вести от середины задний части. Ставим маркер на 14-ую петлю, от нее отсчитываем 26 петель и ставим маркер на 27-ю п., ещё раз отсчитываем 26 петель и ставим маркер на 27-ю п. и так далее по кругу, до конца кругового ряда. Лучше, чтобы первый маркер отличался по цвету.

Убавки делаем следующим образом :

11 п. провязываем изнаночными, 12-ю п. снимаем на спицу, 13-ю провязываем изнаночной, затем 12-ю п. набрасываем на 13-ю. Петлю с маркером (14-ю)провязываем изнаночной.

1-ю п. следующего (бокового) клина провязываем изнаночной, затем возвращаем её на левую спицу. 2-ю п. набрасываем на первую, и переснимаем первую петлю на правую спицу.

Далее провязываем 22 п. по рисунку (11 изн. п. и 11 лиц п.).

23-ю п. снимаем на спицу, 24-ю провязываем лицевой, затем 23-ю п. набрасываем на 24-ю. Петлю с маркером провязываем лицевой.

1-ю п. следующего (переднего) клина провязываем лицевой, затем возвращаем её на левую спицу.

2-ю п. набрасываем на 1-ю п. и переснимаем 1-ю п. на правую спицу. Далее провязываем 22 лиц. п. Опять 23-ю п. снимаем на спицу, 24-ю провязываем лицевой, затем 23-ю п. набрасываем на 24-ю. Петлю с маркером провязываем лицевой.

1-ю п. следующего (бокового) клина провязываем лицевой, затем возвращаем её на левую спицу.

2-ю п. набрасываем на 1-ю п. и переснимаем 1-ю п. на правую спицу.

Далее провязываем 22 п. по рисунку (11 лиц п. и 11 изн. п.), 23-ю п. снимаем на спицу, 24-ю п. провязываем изнаночной, затем 23-ю п. набрасываем на 24-ю. Петлю с маркером провязываем изнаночной.

1-ю п. следующего (заднего) клина провязываем изнаночной, затем возвращаем её на левую спицу, 2-ю п. набрасываем на первую, и переснимаем первую петлю на правую спицу. Довязать 11 п. изнаночными.

Плавно переходим на чулочные спицы. Так будет проще делать убавки.

Следующий ряд провязать по рисунку без убавок. Убавки делать через ряд, в начале и в конце каждого клина.

Так провязываем до момента когда между петлями с маркерами останется по 3 петли (вместо 26-и). В следующем ряду провязываем эти 3 петли вместе. На спицах останется 8 п. Спускаем их на нить и стягиваем.

Закрепить нить. Макушка готова.

Сделать отворот у шапки нужной ширины.

Если вам понравились эти идеи, ставьте палец вверх и подписывайтесь на канал , это будет лучшей наградой для нас!